GB/音频/声音的构成
人耳所能感受到的声音, 主要由三个因素所构成, 即响度, 音调和音色, 称为声音的三要素. 声音是一种波, 振幅和频率是波的物理描述, 音色则偏向主观.
- 响度: 声音的大小, 决定于物体震动幅度大小(即振幅大小).
- 音调: 声音的高低, 決定于物体震动速度快慢(即频率高低).
- 音色: 声音的特色, 決定于声音的波形.
响度
声波的振幅越大, 响度越大; 振幅越小, 响度越小. 响度的单位是分贝(dB, decibel), 但要注意分贝是一个比例描述, 比如零分贝并不代表没有声音, 而是指人耳能听到的最小声音. 0 分贝相较于 10 分贝, 强度相差 10 倍, 0 分贝相较于 20 分贝, 強度相差 100 倍. 它们之间存在一个对数关系.
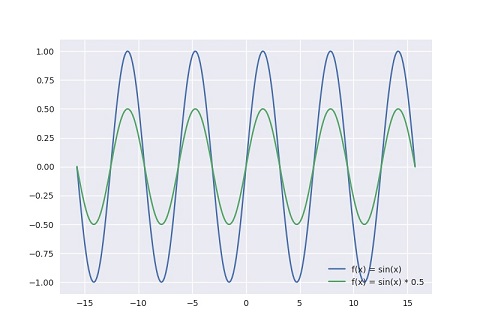
如下是两个频率相同声波的波形, 分别为 f(x)= sin(x) 和 f(x)= 1/2sin(x). 如果不考虑人耳的感知范围, 在人耳听来, 前者会比后者更响.
音调
声波的频率越高, 音调越高, 声音听起来感觉越刺耳; 频率越低, 音调越低, 声音听起来感觉越低沉. 频率低的声音穿透力更强, 比如一到夏天, 许多小区就会出现大量关于邻居家空调外机噪音的投诉, 空调外机发出的噪音其频率就非常低(低频噪音), 因此其穿透性非常好.
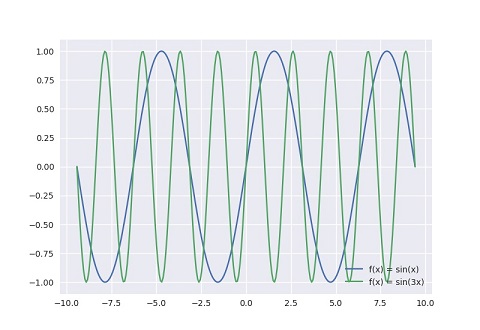
如下是两个频率相同声波的波形, 分别为 f(x)= sin(x) 和 f(x)= sin(3x). 如果不考虑人耳的感知范围, 在人耳听来, 前者会比后者更低沉.
音色
严格来讲音色并不是一个真实的物理量, 音色是许多物理量的叠加. 正是音色才能让人类分别不同的人声和乐声. 在真实世界中, 我们很难接触到像 f(x)= sin(x) 一样如此完美的波形, 听到的声音是许多不同频率和振幅声波的叠加. 但叠加完成后的声波又能表现出波的特性. 如下图所示的波形, 你能明显感觉到它是一个波, 但这个波又有点不同, 因为该波是主波 f(x)= sin(x) 与谐波 f(x)= cos(0.5x) 的叠加:
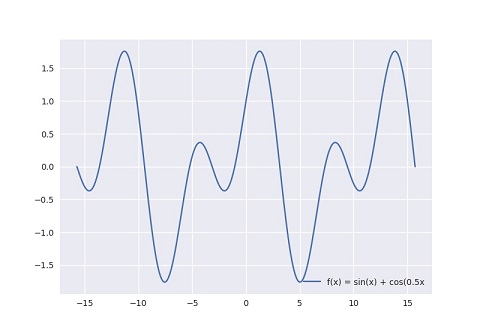
即使频率与振幅都相同的声波, 因为所加入的谐波不同, 所表现出来的音色也不同.
关于如何绘制波形图
本节的图片均由 Python 的 Matplotlib 库生成. Matplotlib 是一个非常经典的绘图库, 常常用于大数据分析与机器学习场景.
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.rcParams.update({'font.size': 22})
ax = plt.subplot()
x = np.linspace(-5*np.pi, 5*np.pi, 256)
ax.plot(x, np.sin(x), label='f(x) = sin(x)')
x = np.linspace(-5*np.pi, 5*np.pi, 256)
ax.plot(x, 0.5 * np.sin(x), label='f(x) = sin(x) * 0.5')
ax.legend(loc='lower right')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.rcParams.update({'font.size': 22})
ax = plt.subplot()
x = np.linspace(-3*np.pi, 3*np.pi, 256)
ax.plot(x, np.sin(x), label='f(x) = sin(x)')
x = np.linspace(-3*np.pi, 3*np.pi, 256)
ax.plot(x, np.sin(3 * x), label='f(x) = sin(3x)')
ax.legend(loc='lower right')
plt.show()
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.rcParams.update({'font.size': 22})
ax = plt.subplot()
x = np.linspace(-5*np.pi, 5*np.pi, 256)
ax.plot(x, np.sin(x) + np.cos(0.5 * x), label='f(x) = sin(x) + cos(0.5x')
ax.legend(loc='lower right')
plt.show()