数字图像处理/空间滤波/高斯滤波
高斯模糊(英语: Gaussian Blur), 也叫高斯平滑, 是在 Adobe Photoshop, GIMP 以及 Paint.NET 等图像处理软件中广泛使用的处理效果, 通常用它来减少图像噪声以及降低细节层次. 这种模糊技术生成的图像, 其视觉效果就像是经过一个半透明屏幕在观察图像, 这与镜头焦外成像效果散景以及普通照明阴影中的效果都明显不同. 高斯平滑也用于计算机视觉算法中的预先处理阶段, 以增强图像在不同比例大小下的图像效果(参见尺度空间表示以及尺度空间实现). 从数学的角度来看, 图像的高斯模糊过程就是图像与正态分布做卷积. 由于正态分布又叫作高斯分布, 所以这项技术就叫作高斯模糊. 图像与圆形方框模糊做卷积将会生成更加精确的焦外成像效果. 由于高斯函数的傅立叶变换是另外一个高斯函数, 所以高斯模糊对于图像来说就是一个低通滤波器.
效果展示

转换函数
高斯模糊是一种图像模糊滤波器, 它用正态分布计算图像中每个像素的变换. N 维空间正态分布方程为
G(r) = [e^(-r²/2σ²)] / (2πσ² ^ N/2)
在二维空间定义为
G(u, v) = 1/(2πσ²) * e^[-(u² + v²)/(2σ²)]
其中 r 是模糊半径(r² = u² + v²), σ 是正态分布的标准偏差. 在二维空间中, 这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆. 分布不为零的像素组成的卷积矩阵与原始图像做变换. 每个像素的值都是周围相邻像素值的加权平均. 原始像素的值有最大的高斯分布值, 所以有最大的权重, 相邻像素随着距离原始像素越来越远, 其权重也越来越小. 这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果.
σ 值介绍
尺度参数 σ 决定了分布幅度, 以下是不同尺度参数 σ 的一维概率密度函数图像, 在高斯模糊处理中, σ 常取 1.5.
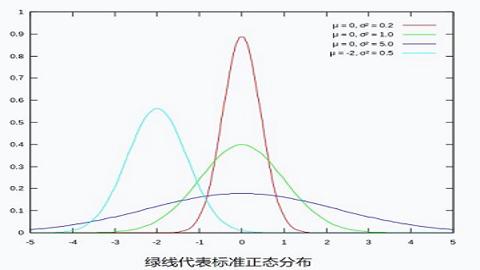
标准正态分布是位置参数 μ = 0, 尺度参数 σ = 1 的正态分布
权重矩阵
根据定义, 写出二维正态分布概率密度函数代码表达式:
import math
def get_cv(r, sigma):
return 1 / (2 * math.pi * sigma ** 2) * math.exp((-r**2) / (2 * sigma ** 2))
取 σ = 1.5, 并假定中心坐标为 (0, 0), 代入公式, 则容易得到包含中心坐标在内的 25(即: 模糊半径 r=2) 个坐标的权重为
[[ 0.01195525 0.02328564 0.02908025 0.02328564 0.01195525]
[ 0.02328564 0.04535423 0.05664058 0.04535423 0.02328564]
[ 0.02908025 0.05664058 0.07073553 0.05664058 0.02908025]
[ 0.02328564 0.04535423 0.05664058 0.04535423 0.02328564]
[ 0.01195525 0.02328564 0.02908025 0.02328564 0.01195525]]
其权重总和等于 0.82914190, 我们需要其权重和为 1, 因此每一项除以 0.82914190 后得到
[[ 0.01441882 0.02808402 0.0350727 0.02808402 0.01441882]
[ 0.02808402 0.05470021 0.06831229 0.05470021 0.02808402]
[ 0.0350727 0.06831229 0.08531173 0.06831229 0.0350727 ]
[ 0.02808402 0.05470021 0.06831229 0.05470021 0.02808402]
[ 0.01441882 0.02808402 0.0350727 0.02808402 0.01441882]]
假设现在有 25 个像素点, 每个像素点都是 (0~255) 的灰度值, 中心坐标灰度值为 200, 其余坐标灰度值均为 10:
[[ 10 10 10 10 10]
[ 10 10 10 10 10]
[ 10 10 200 10 10]
[ 10 10 10 10 10]
[ 10 10 10 10 10]]
每个像素分别乘以权重矩阵, 得到
[[ 0.14418818 0.28084023 0.35072701 0.28084023 0.14418818]
[ 0.28084023 0.54700208 0.68312293 0.54700208 0.28084023]
[ 0.35072701 0.68312293 17.06234604 0.68312293 0.35072701]
[ 0.28084023 0.54700208 0.68312293 0.54700208 0.28084023]
[ 0.14418818 0.28084023 0.35072701 0.28084023 0.14418818]]
对该矩阵求和, 得到 sum = 26, 即高斯模糊后, 中心坐标的灰度值为 26. 可以看到, 相比原先 200 的灰度值, 高斯模糊后的灰度值与周围像素的噪声以及细节层次降低了, 亦即"模糊"了.
如果对 RGB 三个通道分别进行高斯模糊在合并处理, 就能得到模糊后的图像了
代码实现
import math
import numpy as np
import PIL.Image
import PIL.ImageFilter
import scipy.misc
import scipy.signal
# 概率密度函数
def get_cv(r, sigma):
return 1 / (2 * math.pi * sigma ** 2) * math.exp((-r**2) / (2 * sigma ** 2))
# 高斯滤波掩模
def get_window():
# 模糊半径为 2, sigma 为 1.5
radius, sigma = 2, 1.5
window = np.zeros((radius * 2 + 1, radius * 2 + 1))
for i in range(-radius, radius + 1):
for j in range(-radius, radius + 1):
r = (i ** 2 + j ** 2) ** 0.5
window[i + radius][j + radius] = get_cv(r, sigma)
return window / np.sum(window)
def convert_2d(r):
window = get_window()
s = scipy.signal.convolve2d(r, window, mode='same', boundary='symm')
return s.astype(np.uint8)
def convert_3d(r):
s_dsplit = []
for d in range(r.shape[2]):
rr = r[:, :, d]
ss = convert_2d(rr)
s_dsplit.append(ss)
s = np.dstack(s_dsplit)
return s
im = PIL.Image.open('/img/jp.jpg')
im_mat = np.asarray(im)
im_converted_mat = convert_3d(im_mat)
im_converted = PIL.Image.fromarray(im_converted_mat)
im_converted.show()
PIL 版本代码对应如下:
import PIL.Image
import PIL.ImageFilter
im = PIL.Image.open('/img/jp.jpg')
im = im.filter(PIL.ImageFilter.GaussianBlur(radius=2))
im.show()
算法层面可行的优化项:
线性可分性. 二维矩阵变换得到的效果可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到. 从计算的角度来看, 这样只需要 O(n × M × N) + O(m × M × N) 次计算,而不可分的矩阵则需要 O(m x n x M x N) 次计算.
空间换时间. 模糊半径为 2 的权重表仅有 6 个可选权值, 且图像灰度值仅有 256 种. 因此只需预先计算 6 * 256 = 1536 次乘法计算, 之后的所有乘法计算就都能转换为 O(1) 的查表. 使每一个像素点由优化前的 25 次乘法计算 + 24 次加法计算减少为 24 次加法计算.