数字图像处理/直方图均衡化
直方图均衡化处理的中心思想是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布. 直方图均衡化就是对图像进行非线性拉伸, 重新分配图像像素值, 使一定灰度范围内的像素数量大致相同. 直方图均衡化就是把给定图像的直方图分布改变成"均匀"分布直方图分布.
转换函数
假设输入是一张 8 比特灰度图, k 为 0 至 255 之间任一灰度级, n 为灰度为 k 的像素数, m 为图像的总像素数, 则任意灰度级的概率函数为
p(k) = n / m
则原始图像灰度为 k 的像素经过直方图均衡化的结果 s 为:
s = 255 * (p(0) + p(1) + p(2) + ... + p(k))
代码实现
import matplotlib.pyplot as plt
import numpy as np
import PIL.Image
import scipy.misc
def convert_2d(r):
x = np.zeros([256])
for i in range(r.shape[0]):
for j in range(r.shape[1]):
x[r[i][j]] += 1
x = x / r.size
sum_x = np.zeros([256])
for i, _ in enumerate(x):
sum_x[i] = sum(x[:i])
s = np.empty(r.shape, dtype=np.uint8)
for i in range(r.shape[0]):
for j in range(r.shape[1]):
s[i][j] = 255 * sum_x[r[i][j]]
return s
im = PIL.Image.open('/img/jp.jpg')
im = im.convert('L')
im_mat = np.asarray(im)
# 显示输入直方图
plt.hist(im_mat.reshape([im_mat.size]), 256, normed=1)
plt.show()
im_converted_mat = convert_2d(im_mat)
# 显示输出直方图
plt.hist(im_converted_mat.reshape([im_converted_mat.size]), 256, normed=1)
plt.show()
im_converted = PIL.Image.fromarray(im_converted_mat)
im_converted.show()
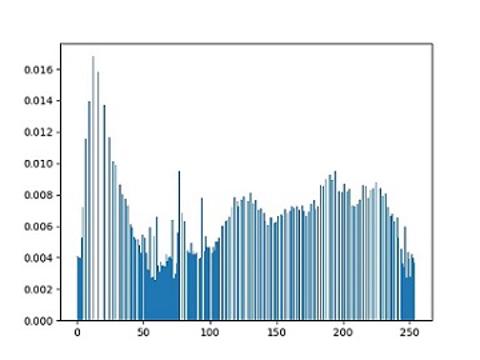
实验效果
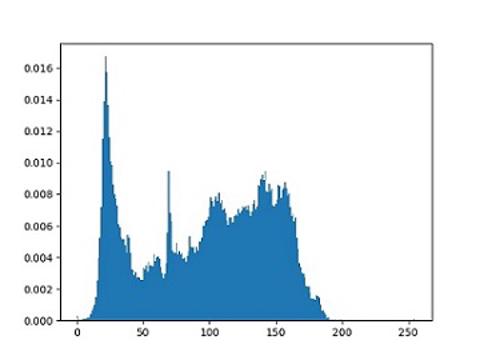
原始直方图
直方图均衡化后的直方图, 可以看到图像分布变得均匀