遗传算法/简单遗传算法

遗传算法是计算数学中用于解决最佳化的搜索算法, 是进化算法的一种. 进化算法最初是借鉴了进化生物学中的一些现象而发展起来的, 这些现象包括遗传, 突变, 自然选择以及杂交等. 这类算法的核心思想源于这样的认识: 生物进化过程是一个自然, 并行和稳健的优化过程. 这一优化过程的目的是对环境的适应性, 生物种群通过优胜劣汰及遗传变异来达到进化目的. 生物的进化通过繁殖, 变异, 竞争和选择这四种基本形式实现的. 因而, 如果把待解决的问题理解为对某个目标函数的全局优化, 则进化算法就是建立在模拟生物种群进化过程基础上的随机搜索优化技术.
遗传算法通常实现方式为一种计算机模拟. 对于一个最优化问题, 一定数量的候选解(称为个体)可抽象表示为基因组, 使种群向更好的解进化. 传统上, 解用二进制表示(即 0 和 1 的串), 但也可以用其他表示方法. 进化从完全随机个体的种群开始, 之后一代一代发生. 在每一代中评价整个种群的适应度, 从当前种群中随机地选择多个个体(基于它们的适应度), 通过自然选择和突变产生新的生命种群, 该种群在算法的下一次迭代中成为当前种群.
名词英文对照
| 中文 | 英文 |
|---|---|
| 遗传算法 | GAs |
| 染色体 | Chromosome |
| 基因 | Gene |
| 基因组 | Genemo |
| 基因座 | Locus |
| 等位基因 | Allele |
| 基因型 | Genetype |
| 表现型 | Phenotype |
| 进化 | Evolution |
| 群体 | Population |
| 个体 | Individual |
| 适应度 | Fitness |
| 遗传算子 | Genetic Operators |
| 选择 | Selection |
| 交叉 | Crossover |
| 变异 | Mutation |
| 交叉概率 | Crossover rate |
| 变异概率 | Mutation rate |
遗传算法整体流程
+--------------+
| 初代群体 |
+-------+------+
|
+-------v------+
| 个体评价 +<----------------+
+-------+------+ |
| |
+-------v------+ |
| 选择运算 | |
+-------+------+ |
| |
+-------v------+ |
| 交叉运算 | |
+-------+------+ |
| |
+-------v------+ |
| 变异运算 | |
+-------+------+ |
| |
+-------v------+ |
| 子代群体 +-----------------+
+--------------+
- 随机生成 M 个个体的基因型作为初始群体. 一种通用的方法是使用固定长度的二进制字符串表示基因.
- 计算群体的个体适应度. 基因是随机的, 但是"基因是否适应环境"须由算法的设计者进行设计. 评价基因的函数被称为适应度函数, 通常返回一个浮点数, 返回数字越高, 说明该基因越适应环境.
- 选择运算. 从当前群体中选择一部分个体进入子代, 个体的适应度越高, 被选取的概率越大.
- 交叉运算. 子代个体两两配对, 互相交换部分基因.
- 变异运算. 以一定的概率随机改变每个个体的基因.
- 终止条件判断. 若未到达终止条件, 回到步骤二; 否则以进化过程中所得到的具有最大适应度的个体作为最优解, 结束算法.
遗传算法手工模拟
我们使用一个实际的例子来演示下遗传算法的各个步骤. 现有山羊种群, 其中有有角和无角, 黑色和白色两种性状. 由于全球进入冰河期, 毛色越黑, 角越小的山羊存活率和繁殖率更高. 下面通过遗传算法求解最适合环境的山羊性状.
- 个体编码 我们使用二进制字符串表示基因, 第一个基因座表示有角和无角, 第二个基因座表示黑色和白色. 因此, 有角白羊可表示为 10, 无角白羊可以表示为 00.
- 生成初代群体 遗传算法是对群体的进化操作, 需要准备一些表示起始搜索点的初始群体数据. 原则上, 群体越大, 基因越分散越好. 本例中, 群体大小取 4, 初始群体为 [00, 10, 11, 00].
- 个体评价 遗传算法以个体适应度的大小评价基因的优劣, 从而决定其遗传机会的大小. 适应度函数需要设计者手工设计, 我们可以假定毛发的颜色比起角的大小来说对山羊的存活更加重要, 此时我们简单的将该群体的适应度表达为 [0.25, 0, 0.5, 0.25].
- 选择运算 适应度越高的个体传到子代的概率越大, 二号个体此时适应度为 0, 而三号个体此时适应度为 0.5 为最高. 在子代中, 三号个体的基因复制了两遍而二号个体的基因被淘汰. 此时群体为 [00, 11, 11, 00].
- 交叉运算 个体两两配对, 有一定的概率发生基因的随机交换. 例如, 一号个体和二号个体的基因 00 与 11 发生交叉操作, 变更为 01 与 10. 此时群体为 [01, 10, 11, 00].
- 变异运算 变异运算对个体的某一个或某一些基因座上的基因值按某一较小的概率进行随机改变, 它是产生新的基因和个体的重要方式. 但是若变异的过于频繁, 也容易失去优秀的个体. 我们假定四号个体的毛色基因发生了变异, 此时群体为 [01, 10, 11, 01].
在新产生的子代中, 出现了基因为 01 的个体, 即无角黑色山羊, 而该基因型在初始群体中是不存在的. 需要说明的是, 通常情况下基因远比我们模拟的要复杂, 也不太可能在一次循环中正好找出最优的基因型, 可能需要循环一定的次数才能达到最优结果.
遗传算法运行参数
通常每个遗传算法都必须包含以下四个参数, 这四个运行参数对遗传算法的求解结果和求解效率都有一定的影响, 但目前并没有合理的算则它们的理论依据, 更多的是一种工程经验.
- M: 种群大小, 一般取 20-100
- T: 终止进化代数, 一般取 100-500
- PC: 交叉概率, 一般取 0.4-0.99
- PM: 变异概率, 一般取 0.0001-0.1
示例
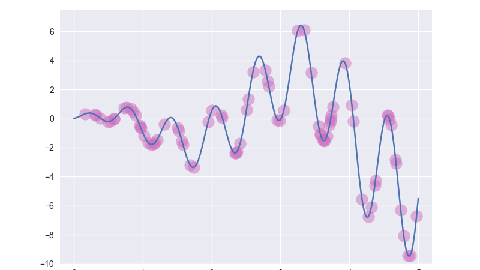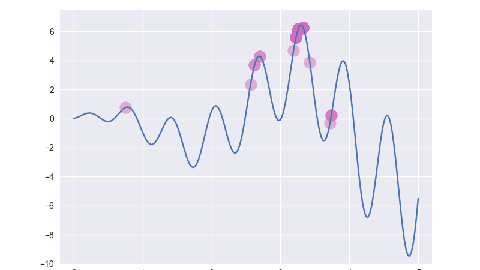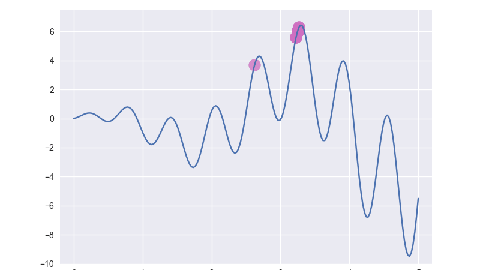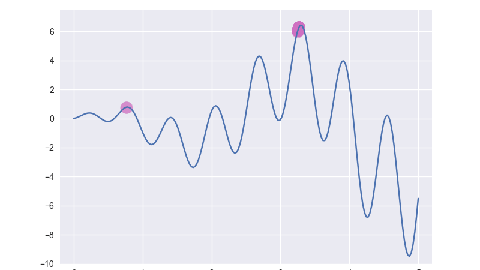
例: 求 f(x)=sin(10x) * x + cos(2x) * x 在 [0, 5] 区间内的最大值.
解:
- 确定基因型的编码与解码方式. 此处使用 10 位二进制编码表示 x 的范围, 即基因型 0000000000 表示 x=0, 基因型 1111111111 表示 x=5.
- 确定个体评价方法. 此处直接使用 f(x) 作为个体适应度评价.
- 设定遗传算子运行参数.
import math
import matplotlib.pyplot as plt
import numpy as np
import random
import typing
class Ga:
def __init__(self) -> None:
self.pop_size = 80
self.max_iter = 20
self.pc = 0.6
self.pm = 0.001
self.dna_size = 10
self.x_bounds = [0, 5]
def encode(self, feno: float) -> typing.List[int]:
a = feno / (self.x_bounds[1] - self.x_bounds[0]) * (2 ** self.dna_size - 1)
a = int(a)
s = bin(a)[2:]
s = '0' * (self.dna_size - len(s)) + s
return [int(e) for e in s]
def decode(self, gene: typing.List[int]) -> float:
s = ''.join([str(e) for e in gene])
return int(s, 2) / (2**self.dna_size - 1) * self.x_bounds[1]
def assess(self, feno: float) -> float:
return math.sin(10 * feno) * feno + math.cos(2 * feno) * feno
def select(self, pop: typing.List[typing.List[int]], fit: typing.List[float]) -> typing.List[typing.List[int]]:
fit_min = min(fit)
fit_max = max(fit)
fit = [(e - fit_min) + fit_max / 2 + 0.001 for e in fit]
return [e.copy() for e in random.choices(pop, fit, k=self.pop_size)]
def crossover(self, pop: typing.List[typing.List[int]]) -> typing.List[typing.List[int]]:
ret = [e.copy() for e in pop]
for i in range(0, self.pop_size, 2):
j = i + 1
if random.random() < self.pc:
p = random.randint(1, self.dna_size-1)
ret[i][p:] = pop[j][p:]
ret[j][p:] = pop[i][p:]
return ret
def mutate(self, pop: typing.List[typing.List[int]]) -> typing.List[typing.List[int]]:
ret = [e.copy() for e in pop]
for i in range(self.pop_size):
e = ret[i]
for j in range(self.dna_size):
if random.random() < self.pm:
e[j] = 1 - e[j]
return ret
def evolve(self) -> typing.Iterable[typing.List[typing.Tuple[typing.List[int], float, float]]]:
pop = [[random.randint(0, 1) for _ in range(self.dna_size)] for _ in range(self.pop_size)]
per = [self.decode(e) for e in pop]
fit = [self.assess(e) for e in per]
yield list(zip(pop, per, fit))
for _ in range(self.max_iter - 1):
pop = self.select(pop, fit)
pop = self.crossover(pop)
pop = self.mutate(pop)
per = [self.decode(e) for e in pop]
fit = [self.assess(e) for e in per]
yield list(zip(pop, per, fit))
plt.style.use('seaborn-v0_8-darkgrid')
plt.figure(figsize=(4.8, 2.7))
ga = Ga()
for i, e in enumerate(ga.evolve()):
p = plt.subplot()
p.set_xlim(-0.2, 5.2)
p.set_ylim(-10, 7.5)
x = np.linspace(ga.x_bounds[0], ga.x_bounds[1], 200)
y = [ga.assess(e) for e in x]
p.plot(x, y)
x = [f[1] for f in e]
y = [f[2] for f in e]
p.scatter(x, y, s=50, c='#CF6FC1', alpha=0.5)
plt.savefig(f'/tmp/img/{i+1:0>2}.png')
p.clear()